Breadth First Search or BFS for a Graph

Breadth First Search (BFS) is a fundamental graph traversal algorithm. It begins with a node, then first traverses all its adjacent. Once all adjacent are visited, then their adjacent are traversed. This is different from DFS in a way that closest vertices are visited before others. We mainly traverse vertices level by level. A lot of popular graph algorithms like Dijkstra’s shortest path, Kahn’s Algorithm, and Prim’s algorithm are based on BFS. BFS itself can be used to detect cycle in a directed and undirected graph, find shortest path in an unweghted graph and many more problems.

Table of Content

• BFS from a Given Source:
  • How Does the BFS Algorithm Work?

  BFS from a Given Source:

  The algorithm starts from a given source and explores all reachable vertices from the given source. It is similar to the Breadth-First Traversal of a tree . Like tree, we begin with the given source (in tree, we begin with root) and traverse vertices level by level using a queue data structure. The only catch here is that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array.

  Initialization: Enqueue the given source vertex into a queue and mark it as visited.

  1. Exploration: While the queue is not empty:
     • Dequeue a node from the queue and visit it (e.g., print its value).
     • For each unvisited neighbor of the dequeued node:
       • Enqueue the neighbor into the queue.
       • Mark the neighbor as visited.
  2. Termination: Repeat step 2 until the queue is empty.

  This algorithm ensures that all nodes in the graph are visited in a breadth-first manner, starting from the starting node.

  How Does the BFS Algorithm Work?

  Let us understand the working of the algorithm with the help of the following example where the source vertex is 0 .

  Step1: Initially queue and visited arrays are empty.

  

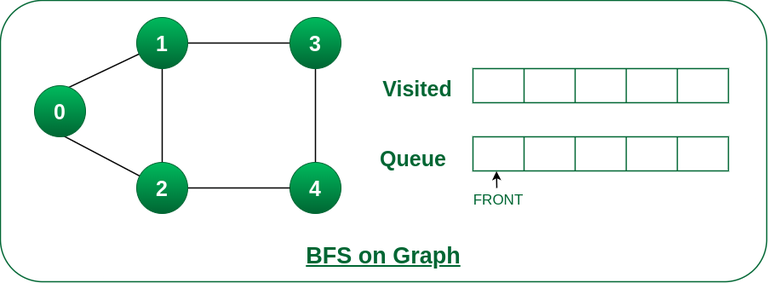
  Queue and visited arrays are empty initially.

  Step2: Push 0 into queue and mark it visited.

  

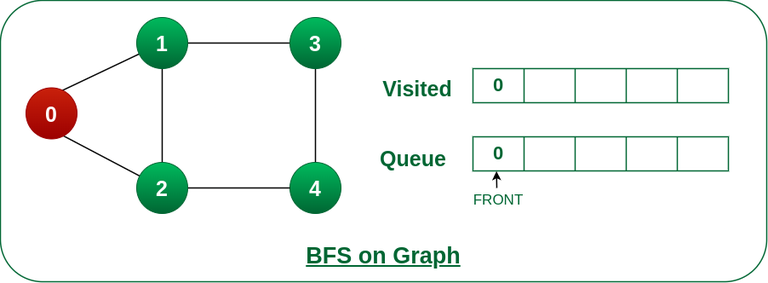
  Push node 0 into queue and mark it visited.

  Step 3: Remove 0 from the front of queue and visit the unvisited neighbours and push them into queue.

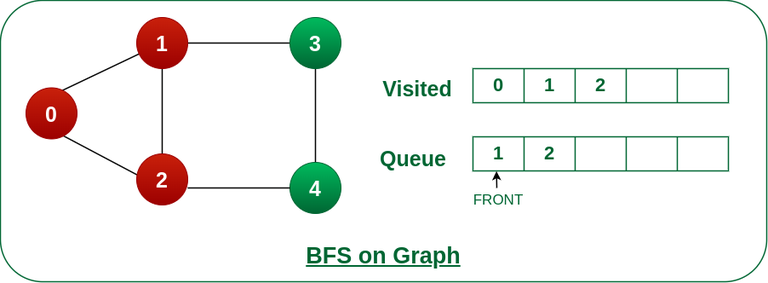  unvisited neighbours and push into queue." width="inherit" height="inherit" />

  Remove node 0 from the front of queue and visited the unvisited neighbours and push into queue.

  Step 4: Remove node 1 from the front of queue and visit the unvisited neighbours and push them into queue.

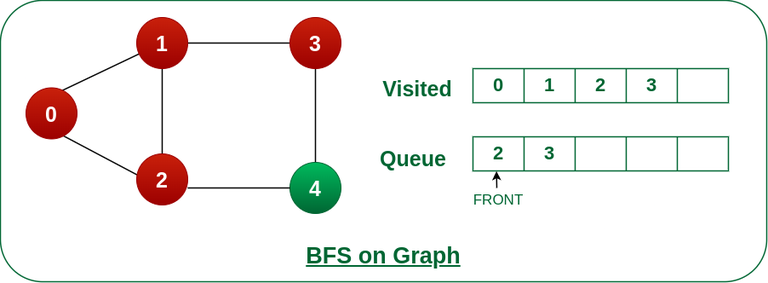  unvisited neighbours and push" width="inherit" height="inherit" />

  Remove node 1 from the front of queue and visited the unvisited neighbours and push

  Step 5: Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

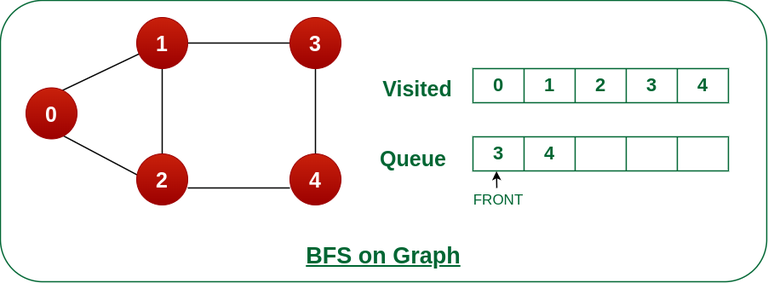  unvisited neighbours and push them into queue." width="inherit" height="inherit" />

  Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

  Step 6: Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue.
  As we can see that every neighbours of node 3 is visited, so move to the next node that are in the front of the queue.

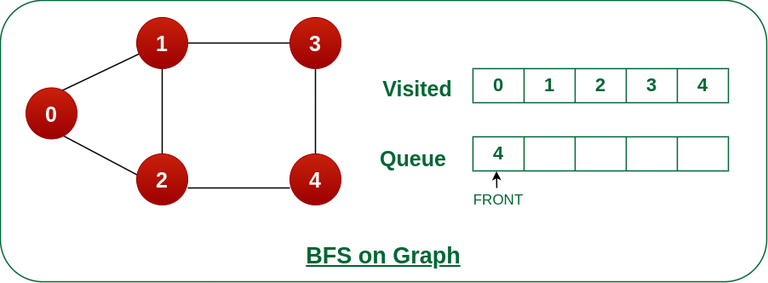  unvisited neighbours and push them into queue. " width="inherit" height="inherit" />

  Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue.

  Steps 7: Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.
  As we can see that every neighbours of node 4 are visited, so move to the next node that is in the front of the queue.

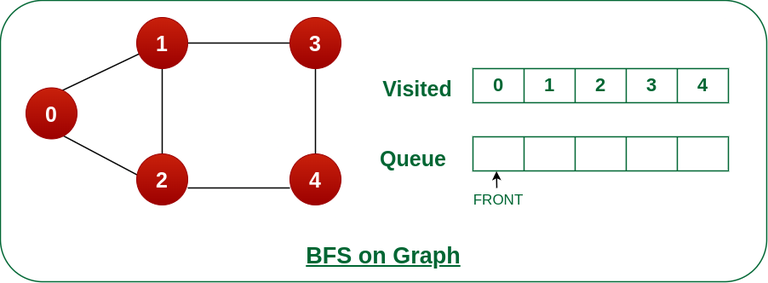  unvisited neighbours and push ithem into queue. " width="inherit" height="inherit" />

  Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.

  Now, Queue becomes empty, So, terminate these process of iteration.

  To deepen your understanding of BFS and other essential algorithms, consider enrolling in our comprehensive course, Tech Interview 101 – From DSA to System Design . This course covers data structures and algorithms from basic to advanced levels , providing you with the skills needed to excel in technical exams and interviews. Building a strong foundation in these concepts is crucial for your success in the tech industry.

             create a new node                                                                                              adjacent vertices of the dequeued vertex                                                                                              Java

                                             adjacent vertices of the dequeued                                                                                             Python